파게로그
[백준 1912, 1749번] 연속합, 점수따먹기 본문
문제 링크: 1912번 연속합, 1749번 점수따먹기
https://www.acmicpc.net/problem/1912
https://www.acmicpc.net/problem/1749
1912번과 1749번을 풀기 위해서는 두 가지 개념을 동시에 사용해야 한다. 두 개념 모두 memoization의 기법이지만 이 문제들에서는 서로 다른 용도로 이용된다. 첫째는 누적 합이고, 둘째는 이전의 값들을 포함시킬지 말지 고려하여 최댓값을 갱신해나가는 것이다.
1. 누적 합을 통해 O(N3)을 O(N2)으로 줄이기
1912번을 나이브하게 푼다고 하면, 연속된 수 몇 개를 선택한 수열의 시작 인덱스 s와 끝 인덱스 e를 O(N2)으로 잡은 후, 해당 경우마다 [s, e] 구간의 모든 원소의 합을 구해주면 된다. 하지만 [s, e] 구간의 모든 원소의 합을 매번 구하는 것은 굉장히 비효율적인데, 최악의 경우 s가 초항, e가 말항을 가리킨다고 하면, 한 번의 합을 구하기 위해 N번을 모두 탐색해야 하기에 곧 O(N3)의 알고리즘이 되는 셈이기 때문이다. 이를 해결하기 위해서 누적 합을 이용한다. 미리 i번째 원소까지의 합을 저장해두고 있는 누적 합 배열을 만들어두면, s, e를 정한 후 해당 구간의 부분 합을 구할 때에 O(1)의 시간만이 소요된다.
2. 이전의 값들을 포함시킬지 말지 고려하여 최댓값을 갱신함으로써 O(N2)를 O(N1)으로 줄이기
하지만 누적 합을 이용하더라도 결국 O(N2)의 과정이 남아있다. 하지만 문제에서 주어진 N은 100,000으로서, 이를 보다 최적화해야한다.
2 1 -4 3 4 -4 6 5 -5 1
dp[i]에는, a[i]를 구간에 반드시 포함시킨다는 전제 하에, 구간의 합의 최댓값을 저장한다. 앞의 원소부터 순차적으로 탐색해나가면서 그 과정을 보면 다음과 같다.
1. a[0]
dp[0] = 2
2. a[1]
지금까지의 합, 즉 dp[0]을 포함하는 편이 좋을까? 아니면 새로 시작하는 게 좋을까?
포함하는 게 좋다.
dp[1] = dp[0] + a[1] = 3
3. a[2]
지금까지의 합, 즉 dp[1]을 포함하는 편이 좋을까? 아니면 새로 시작하는 게 좋을까?
포함하는 게 좋다.
dp[2] = dp[1] + a[2] = -1
여기서 헷갈릴 수 있는데, a[2]는 음수이기 때문에 왜 포함하냐는 생각이 들 수 있다. 하지만 dp[i]의 정의는 'a[i]를 구간에 반드시 포함시킨다는 전제 하에, 구간의 합의 최댓값'이기 때문에 dp[2]에는 a[2]를 포함시키지 않을 수 없다. 다만 a[2]가 음수이기 때문에 구간에서 제외해야 한다는 사실은 a[2] 이후, 즉 a[3]에서 나타날 것이다.
4. a[3]
지금까지의 합, 즉 dp[2]를 포함하는 편이 좋을까? 아니면 새로 시작하는 게 좋을까?
포함하지 않는 게 좋다.
dp[3] = a[3]
구간에 a[3] 이전의 것들을 포함하면 손해가 발생하기 때문에, dp[2]를 '손절'하고, a[3]부터 새로 구간을 시작하는 것이다.
일련의 과정을 거친 이후에 dp 배열을 순회하면서, 최댓값을 찾으면 된다.
이 원리는 1749번 점수따먹기 문제에도 똑같이 적용할 수 있다.
이 문제를 가장 원시적으로(?) 해결하면 O(N6)의 알고리즘을 작성할 수 있다. 부분행렬의 최상단 좌측 원소의 위치를 임의로 잡고, 최하단 우측 원소의 위치를 임의로 잡는다. ①각각 행, 열에 대해서 선택하는 과정을 고려하면 O(N4)의 과정이다. 그리고 각각의 경우에 대해, ②해당 부분행렬의 모든 원소의 합을 구하는 데에 N2번이 소요되므로 시간복잡도는 O(N6)이 되는 것이다.
하지만 누적 합 개념을 이용하여 ②의 과정을 O(1)로 최적화하여 전체 시간복잡도를 O(N4)로 줄일 수 있다. 실제로 자바로도 O(N4) 코드가 통과하는 것을 확인하기는 했으나, N과 M이 200 미만이라는 범위를 고려하면 이는 바람직하지도 않을 뿐더러, 실제로도 아직 개선의 여지가 있다. 여기에서 위의 두 번째 개념을 이용하는 것이다.
행이든 열이든, 즉 가로이든 세로이든 임의로 한 구간을 잡는다.

위의 예시에서 파란색 부분으로 임의의 열의 구간을 지정한 경우에 대해 생각해보자. 이를 누적 합 배열로 보면 다음과 같다.

위의 예시에서, 선택한 열의 구간에 대해서, 해당 행까지의 누적 합을 구해서 표시하면 다음과 같다.
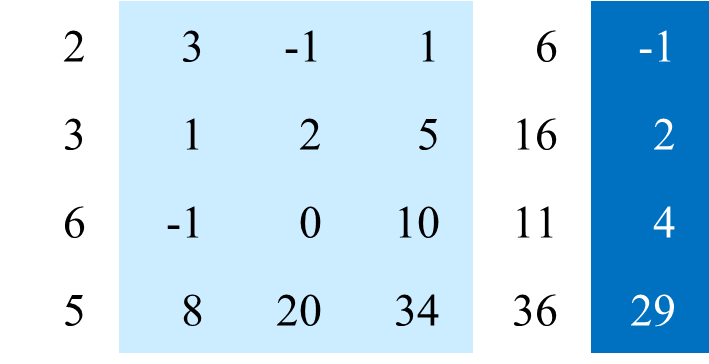
즉 파란색 부분을 s[0], s[1], s[2], ...라고 한다면, 이제 우리가 하고자 하는 것은 1912번을 푸는 것과 완벽히 동일하다. 다만 dp 배열을 직접 사용하지는 않는다. 최댓값만 알면 되기 때문이다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int rows = Integer.parseInt(st.nextToken());
int cols = Integer.parseInt(st.nextToken());
long[][] m = new long[rows + 1][cols + 1];
for (int i = 1; i <= rows; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j = 1; j <= cols; j++) {
m[i][j] = Integer.parseInt(st.nextToken());
}
}
for (int i = 1; i <= rows; i++) {
for (int j = 1; j <= cols; j++) {
m[i][j] = m[i - 1][j] + m[i][j - 1] - m[i - 1][j - 1] + m[i][j];
}
}
long mx = Long.MIN_VALUE;
for (int c1 = 1; c1 <= cols; c1++) {
for (int c2 = c1; c2 <= cols; c2++) {
long last = 0; // dp[r - 1]과 동일한 역할
for (int r = 1; r <= rows; r++) {
// [c1, c2]열 내에서 [r]행의 원소의 합
long sum = m[r][c2] - m[r][c1 - 1] - m[r - 1][c2] + m[r - 1][c1 - 1];
// 이전 행까지의 합을 포함할 것인지, 이번 행부터 새로 시작할 것인지 선택
last = max(last + sum, sum);
// mx 갱신
mx = max(mx, last);
}
}
}
System.out.println(mx);
}
static long max(long a, long b) {
return a > b ? a : b;
}
}'콤퓨타 왕왕기초 > PS' 카테고리의 다른 글
| [백준 1520번] 내리막 길 (0) | 2022.03.16 |
|---|---|
| [백준 1188번] 음식 평론가 (0) | 2022.03.15 |
| [백준 11066번] 파일 합치기 (0) | 2022.02.15 |
| [백준 10775번] 공항 (0) | 2022.02.13 |
| binary search and parametric search (1) | 2022.02.06 |
